What is the difference between V(s) and Q(s,a)?
State value function $V(s)$ expresses how well the agent expects to do when it acts normally. $Q(s, a)$ is a counterfactual function that expresses how well the agent expects to do if it first takes some potentially alternative action before acting normally.
A more precise definition
Before making that more precise, let’s add a point of clarity. Value functions (both V and Q) are always with respect to some policy $\pi$. To indicate that they are with respect to policy $\pi$, we often write them as $V^\pi(s)$ and $Q^\pi(s)$. In the case when we’re talking about the value functions for the optimal policy $\pi^*$, we often use the shorthand $V^*(s)$ and $Q^*(s, a)$. Sometimes in literature we leave off the $\pi$ or $*$ and just refer to $V$ and $Q$, because it’s implicit in the context. Regardless, every value function is always with respect to some policy.
With that in mind, let’s give the more precise definitions.
- $V^\pi(s)$ expresses the expected value of the (discounted) future return when following policy $\pi$ from state $s$.
- $Q^\pi(s, a)$ expresses the expected value of the (discounted) future return when first taking action $a$ from state $s$ and then following policy $\pi$ after that first step.
While $V$ tells you how good your policy is, the Q-function lets you evaluate how good it is to take alternative actions for the first time step .1
An example
To illustrate this difference, consider the below three-state MDP where the agent can go left or right and receives -1 reward until it reaches the terminating goal on the right. The straight blue arrows indicate the optimal policy always going to the right.
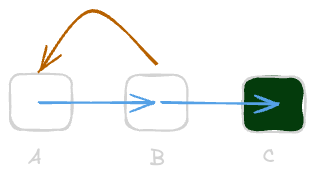
A Three-state MDP to illustrate the difference between Q and V
The state value for any of the states can be easily determined by counting the number of blue arrows until the goal is reached. E.g., $V^\pi(B) = -1\ $ because it is just one step away from the goal. Similarly, the Q-value $Q^\pi(B, \mathrm{right}) = -1$, because the right action is the same action our policy selects. However, we can also evaluate the Q-value for the alternative left action. In this case, $Q^\pi(B, \mathrm{left}) = -3$, because first the agent will go left (following the off-policy orange arc) to state $A$, and then after that step it will follow the blue arcs of our policy back to state $B$ and then to final state $C$.
Why Q is useful
The above example illustrates the difference between Q and V. However, in that example, knowing the Q-value for the bad action wasn’t especially useful, so you may be wondering why we care about Q-values. The reason, of course, is that when the agent starts learning, it will not know the optimal policy. When the policy is suboptimal some of those counterfactual off-policy actions will have higher Q-values then the state value of the current suboptimal policy. When that is the case, knowing which actions have higher Q-values let’s you identify how you can improve your policy.
To illustrate that, let’s have a slightly more complex MDP with a suboptimal policy shown below.
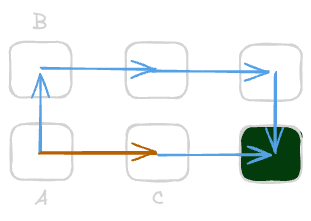
A six-state MDP to illustrate how the Q-function can be used to improve the policy.
In this case, the policy is near optimal except at state A where it goes up to B instead of right to C. Consequently, we have $V(A) = -4\ $. However, the Q-function for counterfactual action “right” shows a better expected return with $Q(A, \mathrm{right}) = -2\ $. This differences indicates that we can improve our policy by setting $\pi(A) = \mathrm{right}$.
There are of course other ways to improve your policy without learning a Q-function, but it is a common a way to do it!
Be careful! $Q^\pi(s, a)$ is not the same as asking what the value is if you change your policy to be $\pi(s) \triangleq a$. It’s asking what the value would be if you took $a$ only on that first step. If the policy eventually returns you to state $s$, the value upon return is evaluated by following what actions the policy would usually select for the state. Our example will help make this clear. ↩︎